De Sāo Paulo, SP.
Quando a gente pensa em matemática, o que vem na cabeça?
📐 Fórmulas complicadas.
📊 Provas de colégio.
😩 E aquela frase clássica: “para quer estudar isso, nunca vai servir pra nada na vida real”.
Pois é, adivinha?
A matemática está em todo lugar.
E muitas vezes salvando o seu dia ou te dando prazer, sem você nem perceber.
Crianças tagarelas no ensino fundamental
Certo dia no final dos anos 1700 em uma escola de Brunswick, cidade do centro-norte da Alemanha localizada no estado da Baixa Saxônia, os alunos do ensino fundamental estavam falando alto demais e fazendo a maior algazarra durante a aula.
Então, para silenciar as crianças, o professor escreveu um problema no quadro negro e pediu que os alunos resolvessem.
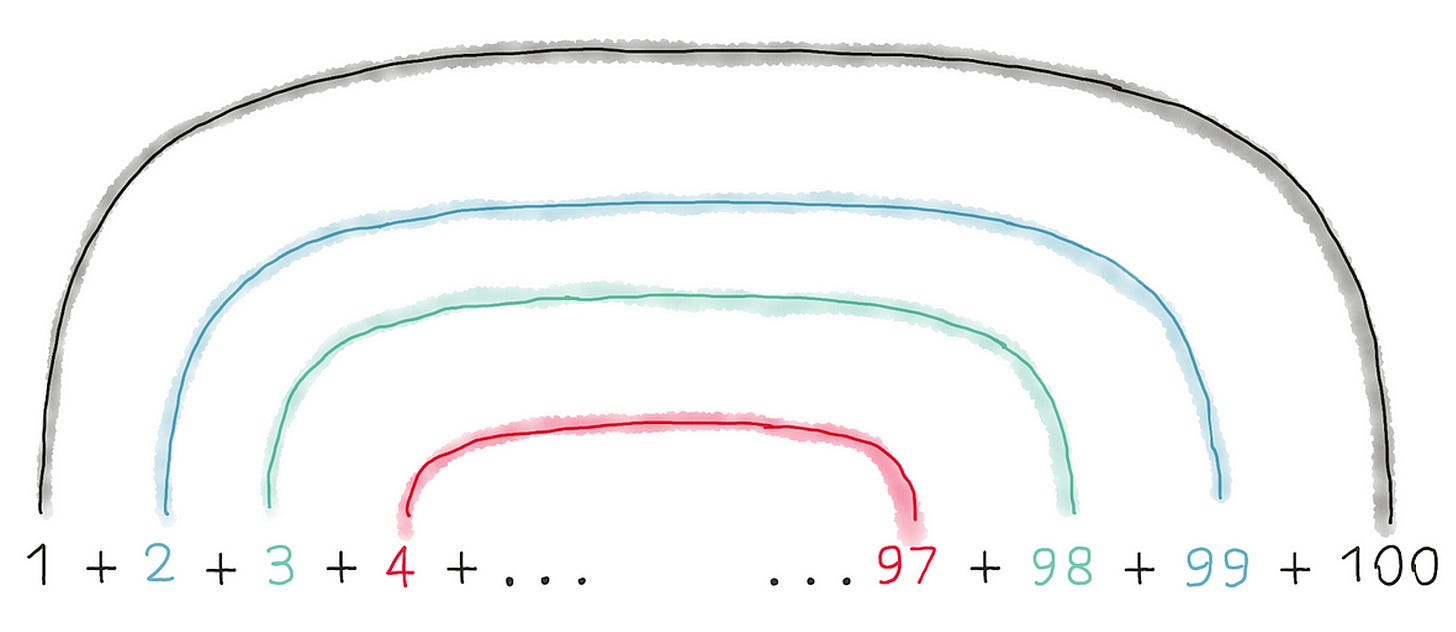
O professor pediu que as crianças somassem todos os números de 1 a 100, imaginando que levaria um bom tempo para elas resolverem o problema, retomando assim o controle da classe.
Mas depois de uns poucos minutos, o pequeno Gauss voltou novamente a tagarelar alegremente com os colegas. O professor, então, perguntou por que Gauss estava falando e este respondeu que já havia resolvido o problema.
Enquanto todos os demais alunos da classe estavam somando os números um a um, Gauss fez algo incomum. Ele percebeu que sempre encontrava 101 se somasse um número na esquerda da sequência com um número da direita.
Por exemplo: 1+100; 2+99; 3+98 ... 50+51, sempre dava 101. Como havia 50 pares de números, Gauss multiplicou 50 x 101 e chegou no resultado certo: 5.050.
O alemão Johann Carl Friedrich Gauss, que viveu entre 1777 e 1855, se tornou mais tarde um dos grandes gênios da matemática.
Genial.
O que parecia uma tarefa impossível virou um cálculo elegante.
Hoje, essa lógica de achar padrões escondidos está por trás de aplicativos que otimizam rotas de entrega, de algoritmos que fazem investimentos e até da música que você ouve no streaming.
Gauss era um gênio e sua forma de pensar ajuda a entender muito sobre o pensamento matemático. O pensamento matemático em si, pode ser aprendido, genialidade é outro departamento.
Guinness, cerveja e estatística 🍺
Corta para a Irlanda do início do final do século XIX.
A cervejaria Guinness queria melhorar a qualidade da bebida, mas como testar ingredientes sem desperdiçar barris inteiros do precioso produto?
Em 1899, a cervejaria Guiness contratou William Sealy Gosset, recém graduado em Oxford com um título que combinava química e matemática.
Ele foi contratado por seus conhecimentos em química, afinal de contas, o que um matemático acrescentaria em uma cervejaria, não é verdade?
Só que a contribuição mais importante de Gosset para a empresa foi usando sua formação matemática, que revolucionou a indústria cervejeira.
Quando o malte moído era preparado para fermentação, uma determinada quantidade de levedura era meticulosamente medida e usada. Leveduras são seres vivos e eram mantidas vivas em recipientes específicos com meio líquido onde se multiplicavam.
Os técnicos pegavam uma amostra do meio líquido e contavam a quantidade de leveduras para saber quanto adicionar à cerveja em fabricação. Tinha que ser uma medida muito controlada, porque poucas leveduras produziriam uma fermentação incompleta; muitas, deixariam a cerveja amarga.
Gosset se questionou o quão exata era aquela medida que os técnicos faziam naquele processo crucial para fabricação da cerveja. Ele fez uma série de medições, analisou os resultados e determinou que a contagem de células de levedura por unidade de volume poderia ser modelada com uma distribuição probabilistica conhecida como Distribuição de Poisson.
Com isso, Gosset foi capaz de criar e implementar regras e métodos de medição que levaram a taxas de concentração de células de leveduras mais exatas do que eram feitas anteriormente.
Usando os métodos matemáticos de Gosset, a cervejaria Guiness passou a fabricar um produto com melhor qualidade e muito mais consistente.
Gosset convenceu seus empregadores a lhe concederem o afastamento de um ano para que ele pudesse estudar com Karl Pearson.
Como a empresa proibia que funcionários publicassem qualquer coisa relacionada ao tema “cerveja”, Gosset adotou academicamente o pseudônimo de “Student”.
Todo estudante de estatística conhece o famoso “Teste t de Student”.
Por trás daquela “cerva” que você bebe com seus amigos nos bares, lá está a matemática e você nem sabia.
Tanques de guerra e números de série
Agora, um salto para a Segunda Guerra Mundial.
Em tempos de guerra, um dos objetivos chave da inteligência militar é determinar o poder de força do inimigo. Por isso, na II Guerra Mundial, os aliados queriam estimar a quantidade dos temidos tanques Panzer que os alemães tinham.
Espionagem? Nem sempre funcionava. A soluçāo veio da matemática.
Para estimar quantos tanques a Alemanha produzia por mês os matemáticos se voltaram para… os números de série das peças capturadas.
Comparando os intervalos, chegaram a estimativas incrivelmente precisas da produção alemã de tanques de guerra.
Mais exatas até do que os relatórios de inteligência da época.
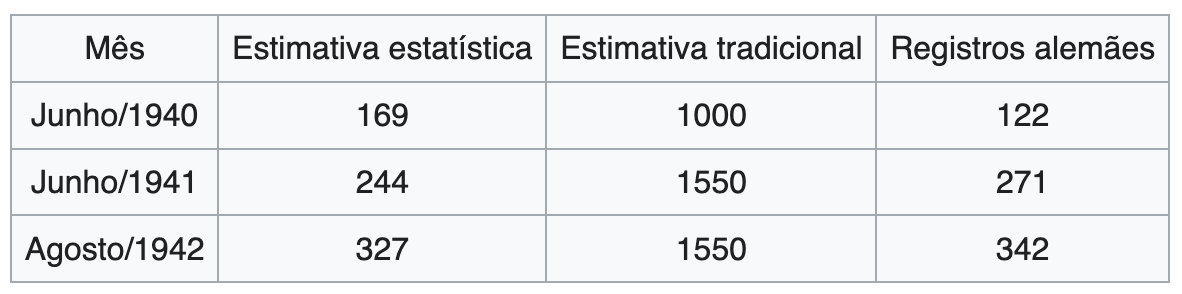
De acordo com as estimativas convencionais da inteligência dos Aliados, os alemães estariam produzindo em torno de 1.400 tanques por mês entre junho de 1940 e setembro de 1942.
Os cálculos estatísticos baseados nos números de série dos tanques capturados, indicou a quantidade como sendo 246 por mês. Após a guerra, registros alemães capturados mostraram que a quantidade real era de 245.
Estimativas para alguns meses específicos são mostradas na tabela abaixo.
Todos veem, mas poucos enxergam
Um dos problemas mais notáveis que a matemática ajudou a resolver, foi o reforço de blindagem nos bombardeiros americanos enviados para as campanhas sobre a Europa durante a II Guerra.
O desafio era aumentar as chances de sobrevivência dos aviões, sem comprometer seu alcance de voo nem sua capacidade de manobra.
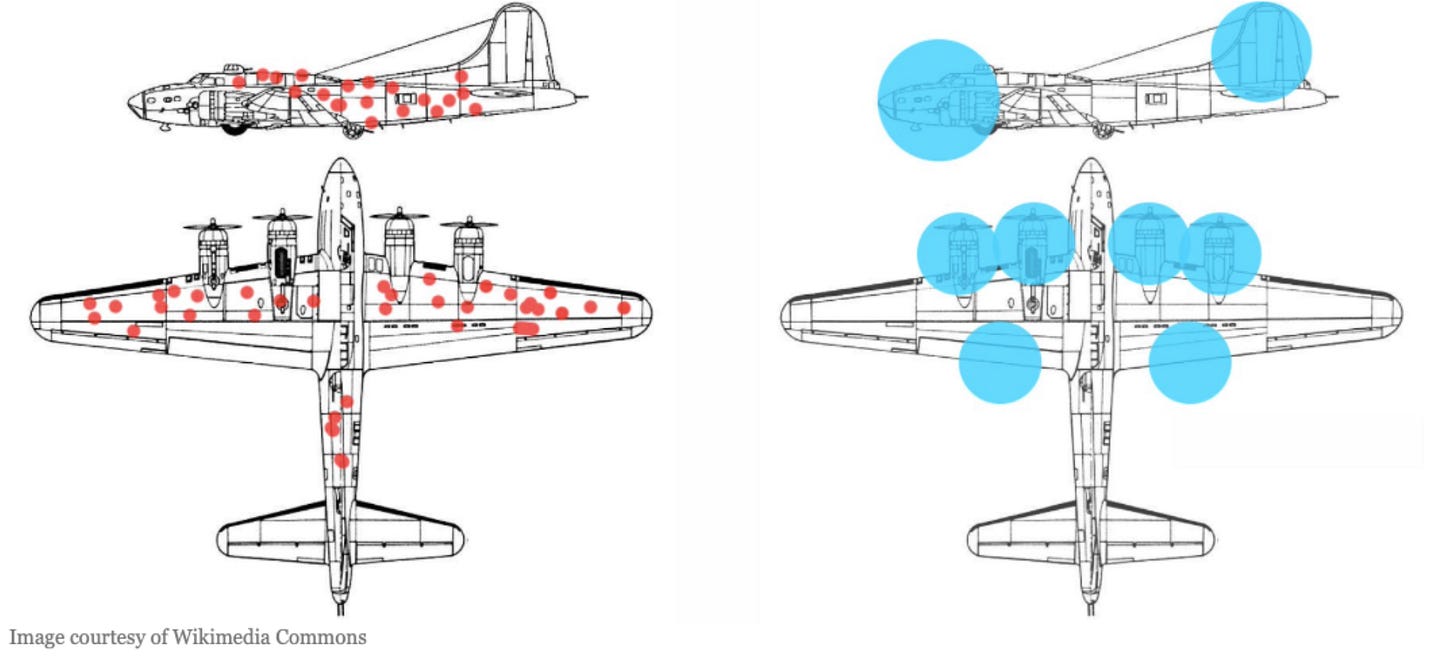
Diante da impossibilidade de cobrir os aviões inteiros com pesadas placas blindadas, era preciso priorizar os locais de colocação das placas. A abordagem adotada pelo foi olhar os bombardeiros B-29 que retornavam das missões de ataque e identificar os locais mais atingidos pelos tiros inimigos.
O pessoal observou que partes da fuselagem - o corpo principal do avião - e das asas tinham praticamente duas vezes mais furos de bala (pontos vermelhos na figura abaixo) do que a plataforma dos motores, da cauda e o nariz dos aviões.
Portanto, foi tomada uma decisão simples: aplicar mais reforço na fuselagem, afinal, era onde a tripulação ficava de modo que fazia mais sentido aplicar proteção extra ali.
No entanto, uma recomendaçāo diferente foi feita por Abraham Wald - um PhD em Matemática pela Universidade da Áustria que integrava o Statistical Research Group – um grupo de pesquisas que aplicava conhecimentos de matemática e estatística para ajudar os americanos a solucionar diversos problemas relacionados a guerra.
Wald indicou que a abordagem sugerida estaria completamente errada. Ao invés disso, ele recomendou que o reforço na blindagem deveria ser feito em todos os locais onde não havia buracos de bala (círculos em azul na figura acima).
Por quê? Porque os únicos aviões analisados foram aqueles que sobreviveram aos ataques e retornaram às bases compondo, portanto, uma amostra exatamente oposta àquilo que o conjunto de dados mostrava a respeito do problema.
Os aviões não estavam retornando com furos de bala nos motores e na cauda porque esses eram abatidos pelos danos nesses locais e caiam no campo de batalha.
Senhores, vocês precisam colocar reforços nas partes onde não há buracos, porque é onde estavam os buracos nos aviões que não voltaram – disse Wald.
Por sorte, a mente matemática de Abraham Wald foi capaz de enxergar além dos dados disponíveis e entender o contexto completo da situação, salvando milhares de vidas nesse processo.
TECONTEI? Por que tudo isso importa pra você
Do planejamento da sua aposentadoria 🍀 ao copo de chope bem tirado 🍻, da sua liberdade até o preço do Uber que você pega no fim do dia 🚗 — a matemática está lá.
É a arte de transformar problemas complicados em soluções simples. O motor invisível que move o mundo.
Então, da próxima vez que alguém soltar um:
“isso é só matemática”,
… responda sem medo:
Só? Nāo! Isso é absolutamente tudo!
Grande abraço,
Eder.
Opiniões: Todas minhas| Fontes: Artigos de minha autoria publicados no Blog do Eder
Disclaimer: Esse artigo foi escrito com uso de IA, baseado em prompts do autor e informações das fontes citadas.












Nenhum comentário:
Postar um comentário